Day 24: Crossed Wires
Megathread guidelines
- Keep top level comments as only solutions, if you want to say something other than a solution put it in a new post. (replies to comments can be whatever)
- You can send code in code blocks by using three backticks, the code, and then three backticks or use something such as https://topaz.github.io/paste/ if you prefer sending it through a URL
FAQ
- What is this?: Here is a post with a large amount of details: https://programming.dev/post/6637268
- Where do I participate?: https://adventofcode.com/
- Is there a leaderboard for the community?: We have a programming.dev leaderboard with the info on how to join in this post: https://programming.dev/post/6631465
Haskell part 2, much better solution
Okay, here’s the outline again - this one ran instantly.
Rather than probing with example values, I took a different approach, debugging the structure. I only really care about inputs and outputs, so I wrote something that turns the “wiring diagram” into a map of label -> Expr, where
data Expr = EInput String | EAnd Expr Expr | EOr Expr Expr | EXor Expr Expr deriving (Show, Ord)(the
Eqinstance is stable in symmatric expressions, eg(==) (EAnd a b) (Eand c d) = a == c && b == d || a == d && b == c)The expressions are grounded in “inputs” (“x00”…“x44”, “y00”…“y44”) - that is, they just expand out all of the intermediary labelled things.
Then I constructed a circuit that I was after by building a non-swapped 44/45-bit full adder, and produced the same set of expressions for those.
Then: for each output, z00…z45, check the “spec” expression against the actual one. If they’re identical, move on.
Otherwise, find some candidate pairs to swap. For these, I considered all possible labelled outputs except “stable” ones - that is, those that were input depdendencies of z_(i-1) - ie, don’t swap any outputs involved in the computation that’s validated thus far.
searchForSwap :: Exprs -> Layout -> String -> Set.Set String -> [(String, String, Layout, Exprs)] searchForSwap eSpec actual zz stable = let vals = Map.keysSet actual & (`Set.difference` stable) & Set.toList ds = dependencies actual in do k1 <- vals k2 <- vals guard $ k1 < k2 guard $ k1 `Set.notMember` (ds Map.! k2) -- don't create any loops guard $ k2 `Set.notMember` (ds Map.! k1) let actual' = swapPair k1 k2 actual eAct' = exprsForLayout actual' guard $ eSpec Map.! zz == eAct' Map.! zz pure (k1, k2, actual', eAct')Taking the new layout with swapped outputs and its corresponding set of expressions, carry on searching as before.
A linear scan over the output bits was all that was required - a unique answer poped out without any backtracking.
Anyway, happy Christmas all.
PS. My other version worked (eventually) - it was following this approach that led me to realise that my “spec” full adder was broken too :-D Never skip the unit tests.
(@CameronDev@programming.dev you were asking about alternatives to graphviz-style approaches I recall)
Yes, I was, and this is very impressive. This should be a generic solution right? I’ll have to work out how to run it and test on my input.
Haskell, programmatic solution
I spent an entire day on this because I didn’t write a unit test to check my “swap outputs” function, which effectively did nothing.
In any case: the approach (which may be more interesting than the code, I know people were interested) involved probing the addition circuit with some example additions - that is, I wrote something that’d let me give alternative inputs from x & y and compute the result using the circuit. I then gave it some simple pairs of values that’d exercise the add and carry bits (ie, pairs chosen from
{i << n, n <- {1..43}, i <- {1, 3}}). That gave me some breaking trials.Because the errors were relatively sparse, I then scanned over pairs of outputs, swapping those that didn’t introduce a data dependency and checking (a) that no new errors were introduced over the trial sets, (b) for any reduction in the number of errors found. I got a bunch fo outputs like this:
swap of ("ccp","mnh") improves matters bad trial count reduced from 346 to 344which found the pairs for me. The search could be improved by more carefully tying the probe inputs to the outputs’ dependencies (ie, if the first error comes from the (xi, yi) input bits, then look for swaps of the dependencies introduced by zi) - but in any case, it finds the answer. Phew.
Rust + Pen and Paper
Yikers. Part 2 took a while, staring at this diagram for hours. Eventually I noticed that each of these blocks has two pairs of (XOR, AND) gates sharing the same inputs (and inputs aren’t changed). So I matched up these pairs based on a distance metric of how much needs to be swapped to fit together. This helped me identify 4 blocks with errors, the rest was solved using pen and paper (one block is missing as it became apparent at that point):
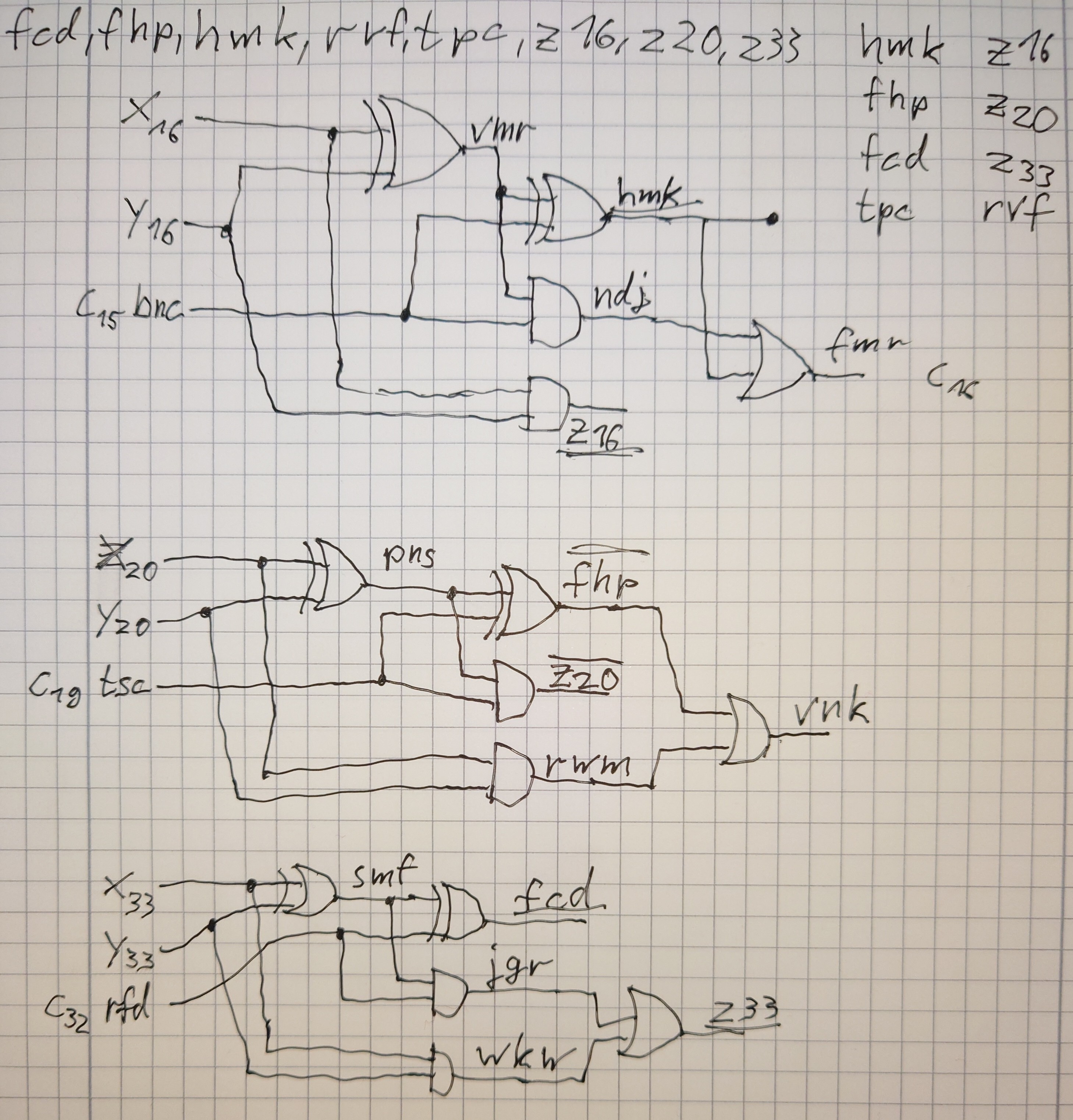
There is also some code, but do yourself and me a favor and don’t look at it. While it does turn up the correct solution, it probably won’t with any other input, especially not the examples.
Haskell bits and pieces
The nice thing about Haskell’s laziness (assuming you use Data.Map rather than Data.Map.Strict) is that the laziness can do a ton of the work for you - you might’ve spotted a few Haskell solutions in earlier days’ threads that use this kind of trick (eg for tabling/memoisation). Here’s my evaluation function:
eval l = let v = l & Map.map (\case Const x -> x And a b -> v Map.! a && v Map.! b Or a b -> v Map.! a || v Map.! b Xor a b -> v Map.! a /= v Map.! b) in vFor part 2, we know what the graph should look like (it’s just a binary adder); I think this is a maximal common subgraph problem, but I’m still reading around that at the mo. I’d love to know if there’s a trick to this.
Thank you for showing this trick, I knew Haskell was lazy but this one blew my mind again.
Yeah, I remember when I saw this for the first time. It’s astonishing how powerful lazy evaluation can be at times.
Javascript
Part one was easy, though despite starting at midnight I only placed 1786 for part one. I think my tendency to want to do OOP makes it take longer…
Part two… Well, I figured it was some sort of binary circuit for trying to add binary numbers. So I hoped that the sum of the x registers and the y registers was the expected result of simulating the circuit like in part one. I later verified that it is the expected result.
I didn’t want to try and manually figure out the bad outputs, coffee wasn’t helping, I wanted sleep. So I uh… I wrote logic to randomly create swaps. And then just hoped RNG got me covered. To help my chances, I ran it on 8 different processes.
When I woke up in the morning I discovered 8 stopped processes, each with “a solution” that was different. Turns out, if you just randomly swap wires at some point you get a system that outputs the desired result - but only because you sufficiently screwed it up more to produce the expected result, even if the system itself would not work for other input.
I could probably change the registers to another value, run it, and see if they match, thus ruling out an incorrect set of swaps causing a correct result with the original binary inputs. But at this point I just decided to do it the manual way following advice on here. My brain is fried, I’m stepping away to take a shower and get ready to visit family.
I had really hoped the bruteforce would work, I modified the bruteforce to run even after it finds a match and I’ll let it run while I’m gone today and see if RNG produces any correct result at some point - I just fear the exponential answer timeout will prevent me from submitting these correctly incorrect combinations lol. I might modify it later with my theory above and just run it on a server indefinitely and see if it produces the correct result eventually.
https://blocks.programming.dev/Zikeji/9e4d6e81595d4845b88cf98eb91852d8
Edit:
Created a raw multithreaded bruteforce variant: topaz
Oh my Kernigan, that was stressful. Really worried about not finishing there.
Considered several approaches, the coolest of which would have been to test individual bits, propagate ‘suspicion’, etc, but it seemed too tricky.
Eventually I needed to go do something other than worry about not finishing so I started writing a validator for the adder structure. Just a couple of rules later I had found 4 faults already and managed to write automated fixups for them!
This means my solver is quite specific to my input but it can potentially be made more complete and I didn’t ‘cheat’ by hardcoding manual graph analysis.
Code
#include "common.h" /* * The approach behind part 2 was to essentially write a bunch of * validation rules for the structure of the adder, and then writing * fixups for problems it would find. That means it's likely quite * tailored to my input, but at least it's not hardcoding manual graph * analysis. */ enum { W_NULL, W_OFF, W_ON }; struct wire; struct wire { struct wire *in[2]; char name[4]; char op; /* [A]ND, [O]R, [X]OR */ int8_t val; /* W_NULL, W_OFF, W_ON */ }; static struct wire wires[320]; static struct wire *zs[46], *swapped[8]; static int nw, nsw; static struct wire * get_wire(const char *name) { int i; for (i=0; i<nw; i++) if (!strcmp(name, wires[i].name)) return &wires[i]; assert(nw < (int)LEN(wires)); assert(strlen(name) < LEN(wires[i].name)); snprintf(wires[nw].name, sizeof(wires[nw].name), "%s", name); return &wires[nw++]; } static int cmp_wires(const void *a, const void *b) { struct wire * const *wa = a; struct wire * const *wb = b; return strcmp((*wa)->name, (*wb)->name); } static int eval(struct wire *wire) { int in1,in2; if (wire->val) return wire->val == W_ON; assert(wire->in[0]); assert(wire->in[1]); in1 = eval(wire->in[0]); in2 = eval(wire->in[1]); wire->val = W_OFF + ( wire->op=='A' ? in1 && in2 : wire->op=='O' ? in1 || in2 : wire->op=='X' ? in1 != in2 : (assert(!"bad op"), -1)); return wire->val == W_ON; } static void swap(struct wire *a, struct wire *b) { struct wire tmp; //printf("swapping %s and %s\n", a->name, b->name); tmp = *a; a->op = b->op; a->in[0] = b->in[0]; a->in[1] = b->in[1]; b->op = tmp.op; b->in[0] = tmp.in[0]; b->in[1] = tmp.in[1]; assert(nsw+2 <= (int)LEN(swapped)); swapped[nsw++] = a; swapped[nsw++] = b; } static struct wire * find_z_xor(int bit) { struct wire *xy_xor; int i; for (i=0; i<nw; i++) { /* must be a XOR */ if (wires[i].op != 'X') continue; /* with an input XOR */ xy_xor = wires[i].in[0]->op == 'X' ? wires[i].in[0] : wires[i].in[1]->op == 'X' ? wires[i].in[1] : NULL; if (!xy_xor) continue; /* connected to the X and Y */ if (xy_xor->in[0]->name[0] != 'x' && xy_xor->in[0]->name[0] != 'y') continue; /* with the same bit number */ if (atoi(xy_xor->in[0]->name+1) != bit) continue; return &wires[i]; } return NULL; } static struct wire * find_xy_and(int bit) { int i; for (i=0; i<nw; i++) { /* must be AND */ if (wires[i].op != 'A') continue; /* must have XY inputs */ if ((wires[i].in[0]->name[0] != 'x' || wires[i].in[1]->name[0] != 'y') && (wires[i].in[0]->name[0] != 'y' || wires[i].in[1]->name[0] != 'x')) continue; /* with the right bit number */ if (atoi(wires[i].in[0]->name+1) != bit || atoi(wires[i].in[0]->name+1) != bit) continue; return &wires[i]; } return NULL; } static void fsck_carry_or(struct wire *or, int bit) { struct wire *wire; int i; /* both inputs must be AND; no fixup if neither */ assert( or->in[0]->op == 'A' || or->in[1]->op == 'A'); for (i=0; i<2; i++) { if (or->in[i]->op == 'A') continue; //printf("carry OR parent %s not AND\n", or->in[i]->name); /* only have fixup for the XY AND */ assert( or->in[!i]->in[0]->name[0] != 'x' && or->in[!i]->in[0]->name[0] != 'y'); wire = find_xy_and(bit); assert(wire); swap(or->in[i], wire); } } static void fsck_z(struct wire *z) { struct wire *wire, *carry_or; int bit; assert(z->name[0] == 'z'); bit = atoi(z->name+1); /* first bit is very different */ if (!bit) return; /* for the final bit, Z is the carry OR */ if (!zs[bit+1]) { /* no fixup if it isn't */ assert(z->op == 'O'); fsck_carry_or(z, bit-1); return; } /* must be a XOR */ if (z->op != 'X') { //printf("Z %s isn't XOR\n", z->name); wire = find_z_xor(bit); assert(wire); swap(z, wire); } /* bit 2 and up must have a carry OR */ if (bit > 1) { carry_or = z->in[0]->op == 'O' ? z->in[0] : z->in[1]->op == 'O' ? z->in[1] : NULL; assert(carry_or); fsck_carry_or(carry_or, bit-1); } } int main(int argc, char **argv) { struct wire *wire; char buf[64], *rest, *lf, *name1,*name2, *opstr; uint64_t p1=0; int bit, i; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); while ((rest = fgets(buf, sizeof(buf), stdin))) { if (!strchr(buf, ':')) break; wire = get_wire(strsep(&rest, ":")); wire->val = W_OFF + atoi(rest); } while ((rest = fgets(buf, sizeof(buf), stdin))) { if ((lf = strchr(buf, '\n'))) *lf = '\0'; name1 = strsep(&rest, " "); opstr = strsep(&rest, " "); name2 = strsep(&rest, " "); strsep(&rest, " "); wire = get_wire(rest); wire->in[0] = get_wire(name1); wire->in[1] = get_wire(name2); wire->op = opstr[0]; } for (i=0; i<nw; i++) if (wires[i].name[0] == 'z') { bit = atoi(&wires[i].name[1]); assert(bit >= 0); assert(bit < (int)LEN(zs)); zs[bit] = &wires[i]; } for (i=0; i < (int)LEN(zs); i++) if (zs[i]) p1 |= (uint64_t)eval(zs[i]) << i; for (i=0; i < (int)LEN(zs); i++) if (zs[i]) fsck_z(zs[i]); qsort(swapped, nsw, sizeof(*swapped), cmp_wires); printf("24: %"PRIu64, p1); for (i=0; i<nsw; i++) printf(i ? ",%s" : " %s", swapped[i]->name); putchar('\n'); return 0; }https://codeberg.org/sjmulder/aoc/src/branch/master/2024/c/day24.c
Btw, spending some time on getting Graphviz output right did make studying the structure much easier!
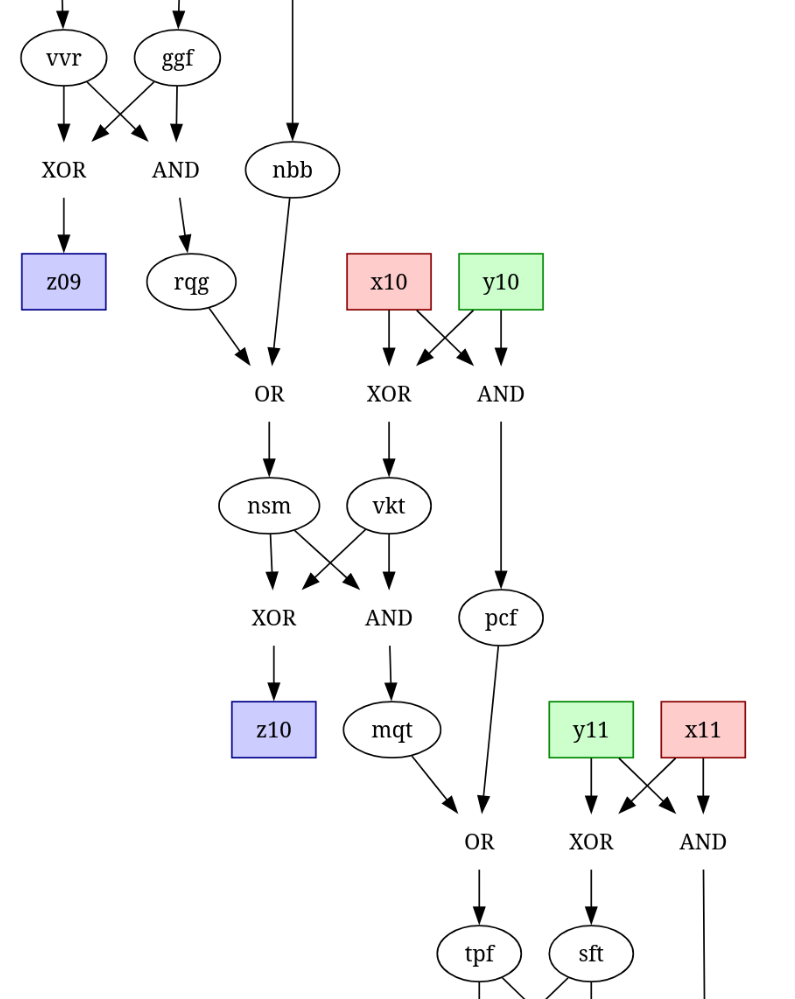
I fiddled for ages to get nice graphviz output, that looks a lot nicer
Dart
Not very happy with this, as for part 2 the code just told me which four pairs of bits of the output needed investigation and I then tediously worked through how they differed from the correct adder implementation in the debugger.
Spoilered as it is overly long and not very interesting.
spoiler
import 'package:collection/collection.dart'; import 'package:more/more.dart'; var nodes = <String, Node>{}; class Node { String name = ''; bool? state; var outputGates = <String>[]; } class Wire implements Node { @override String name; @override bool? state; @override var outputGates = <String>[]; Wire(this.name, this.state); set() { for (var g in outputGates) { (nodes[g]! as Gate).set(); } } } class Gate implements Node { String input1, input2, type; @override String name; @override bool? state; @override var outputGates = <String>[]; Gate(this.name, this.input1, this.input2, this.type); set() { var a = nodes[input1]!.state; var b = nodes[input2]!.state; if (a == null || b == null) return; state = switch (type) { 'AND' => a && b, 'OR' => a || b, _ => a ^ b }; for (var g in outputGates) { (nodes[g]! as Gate).set(); } } } void setup(List<String> lines) { var parts = lines.splitAfter((e) => e.isEmpty); Map<String, Node> wires = Map.fromEntries(parts.first.skipLast(1).map((e) { var p = e.split(': '); return MapEntry(p[0], Wire(p[0], p[1] == '1')); })); nodes = Map.fromEntries(parts.last.map((e) { var p = e.split(' '); return MapEntry(p.last, Gate(p.last, p[0], p[2], p[1])); })); nodes.addAll(wires); for (var g in nodes.values) { if (g is! Gate) continue; nodes[g.input1]!.outputGates.add(g.name); nodes[g.input2]!.outputGates.add(g.name); } } String line(String s) => nodes.keys .where((e) => e.startsWith(s)) .sorted() .reversed .map((e) => nodes[e]!.state! ? '1' : '0') .join(''); part1(List<String> lines) { setup(lines); nodes.values.whereType<Wire>().forEach((e) => e.set()); return int.parse(line('z'), radix: 2); } part2(List<String> lines) { setup(lines); var bits = nodes.keys.count((e) => e.startsWith('x')); for (var b in 0.to(bits)) { nodes.values.whereType<Gate>().forEach((e) => e.state = null); nodes.values.whereType<Wire>().forEach(((e) => e.state = false)); nodes['y${b.toString().padLeft(2, "0")}']!.state = true; nodes.values.whereType<Wire>().forEach((e) => e.set()); print('${line("x")}\t${line("y")}\t${line("z")}\t$b'); var output = line('z'); for (var i in 0.to(bits)) { if (output[bits - i] != ((i == b) ? "1" : "0")) print(i); } } tree('z05'); tree('z06'); // Add break point here and inspect and solve manually using `tree`. print('break here'); } tree(String s, {indent = ''}) { var here = nodes[s]!; if (here is Wire) { print('$indent${here.name} (wire)'); return; } here as Gate; print('$indent${here.name} ${here.type}'); tree(here.input1, indent: indent + '| '); tree(here.input2, indent: indent + '| '); }Haskell
For completeness’ sake. I actually solved part 2 by looking at the structure with Graphviz and checking the input manually for errors. So the code here merely replicates the checks I was doing by hand.
solution
import Control.Arrow import Control.Monad import Data.Bifoldable import Data.Bits import Data.List import Data.Map (Map) import Data.Map qualified as Map import Data.Maybe import Data.Set (Set) import Data.Set qualified as Set import Text.Printf data Op = AND | OR | XOR deriving (Read, Show, Eq) readInput :: String -> (Map String Int, Map String (Op, (String, String))) readInput s = let (inputs, gates) = second (drop 1) $ break null $ lines s in ( Map.fromList $ map (break (== ':') >>> (id *** read . drop 2)) inputs, Map.fromList $ map (words >>> \[a, op, b, _, o] -> (o, (read op, (a, b)))) gates ) evalNetwork :: Map String Int -> Map String (Op, (String, String)) -> Maybe Int evalNetwork inputs gates = fromBits <$> getOutput signals where getOutput = traverse snd . takeWhile (("z" `isPrefixOf`) . fst) . Map.toDescList fromBits = foldl' (\a b -> (a `shiftL` 1) .|. b) 0 signals = Map.union (Just <$> inputs) $ Map.mapWithKey getSignal gates getSignal w (op, (a, b)) = doGate op <$> join (signals Map.!? a) <*> join (signals Map.!? b) doGate AND = (.&.) doGate OR = (.|.) doGate XOR = xor findError :: [(String, (Op, (String, String)))] -> Maybe (String, String) findError gates = findGate AND ("x00", "y00") >>= go 1 . fst where go i carryIn = do let [x, y, z] = map (: printf "%02d" (i :: Int)) ['x', 'y', 'z'] xor1 <- fst <$> findGate XOR (x, y) and1 <- fst <$> findGate AND (x, y) let layer2 = findGates (carryIn, xor1) ++ findGates (carryIn, and1) xorGate2 <- find ((== XOR) . fst . snd) layer2 andGate2 <- find ((== AND) . fst . snd) layer2 let xor2 = fst xorGate2 and2 = fst andGate2 orGate <- find ( \(_, (op, (a, b))) -> op == OR && any (`elem` [a, b]) [xor1, and1, xor2, and2] ) gates msum [ checkIs xor1 =<< otherInput carryIn xorGate2, checkIs z xor2, go (succ i) (fst orGate) ] checkIs p q = (p, q) <$ guard (p /= q) otherInput x (_, (_, (a, b))) | a == x = Just b | b == x = Just a | otherwise = Nothing findGates (a, b) = filter (\(_, (_, ins)) -> ins `elem` [(a, b), (b, a)]) gates findGate op = find ((== op) . fst . snd) . findGates part2 = sort . concatMap biList . unfoldr go . Map.assocs where go gates = (\p -> (p, first (exchange p) <$> gates)) <$> findError gates exchange (a, b) c | c == a = b | c == b = a | otherwise = c main = do (inputs, gates) <- readInput <$> readFile "input24" print . fromJust $ evalNetwork inputs gates putStrLn . intercalate "," $ part2 gatesHaskell
For part2 I compared the bits in the solution of part1 with the sum of x and y. With that, I could check the bits that did not match in a graphviz diagram and work from there.
code
import Control.Arrow import Control.Monad.RWS import Data.Bits (shiftL) import Data.Char (digitToInt) import Data.Functor import Data.List import Data.Map qualified as M import Data.Tuple import Text.ParserCombinators.ReadP hiding (get) import Text.ParserCombinators.ReadP qualified as ReadP type Cable = String data Connection = And Cable Cable | Or Cable Cable | Xor Cable Cable deriving (Show) cable = count 3 ReadP.get eol = char '\n' initial :: ReadP (M.Map Cable Bool) initial = M.fromList <$> endBy ((,) <$> cable <*> (string ": " *> (toEnum . digitToInt <$> ReadP.get))) eol wires = M.fromList <$> endBy wire eol wire = do a <- cable <* char ' ' op <- choice [string "AND" $> And, string "OR" $> Or, string "XOR" $> Xor] b <- char ' ' *> cable c <- string " -> " *> cable return (c, op a b) parse = fst . last . readP_to_S ((,) <$> initial <*> (eol *> wires <* eof)) type Problem = RWS (M.Map Cable Connection) () (M.Map Cable Bool) getConnection :: Connection -> Problem Bool getConnection (And a b) = (&&) <$> getWire a <*> getWire b getConnection (Or a b) = (||) <$> getWire a <*> getWire b getConnection (Xor a b) = xor <$> getWire a <*> getWire b xor True False = True xor False True = True xor _ _ = False getWire :: Cable -> Problem Bool getWire cable = do let computed = do a <- asks (M.! cable) >>= getConnection modify (M.insert cable a) return a gets (M.!? cable) >>= maybe computed return fromBin :: [Bool] -> Int fromBin = sum . fmap fst . filter snd . zip (iterate (`shiftL` 1) 1) toBin :: Int -> [Bool] toBin = unfoldr (\v -> if v == 0 then Nothing else Just (first (== 1) (swap (divMod v 2)))) part1 initial wiring = fst $ evalRWS (mapM getWire zs) wiring initial where zs = filter ((== 'z') . head) . sort $ M.keys wiring part2 initial wiring = fmap fst . filter snd $ zip [0..] (zipWith (/=) p1 expect) where xs = fromBin . fmap (initial M.!) . filter ((== 'x') . head) $ sort $ M.keys initial ys = fromBin . fmap (initial M.!) . filter ((== 'y') . head) $ sort $ M.keys initial zs = filter ((== 'z') . head) . sort $ M.keys wiring p1 = part1 initial wiring expect = toBin $ xs + ys main = getContents >>= print . (fromBin . uncurry part1 &&& uncurry part2) . parseHaskell
Part 1 was trivial, just apply the operations and delay certain ones until you have all the inputs you need.
Code
import Control.Arrow import Data.Bits import Numeric import qualified Data.Char as Char import qualified Data.List as List import qualified Data.Map as Map parse s = (Map.fromList inputs, equations) where ls = lines s inputs = map (take 3 &&& (== "1") . drop 5) . takeWhile (/= "") $ ls equations = map words . filter (/= "") . tail . dropWhile (/= "") $ ls operations = Map.fromList [ ("AND", (&&)) , ("XOR", xor) , ("OR", (||)) ] solveEquations is [] = is solveEquations is (e:es) | is Map.!? input1 == Nothing = solveEquations is (es ++ [e]) | is Map.!? input2 == Nothing = solveEquations is (es ++ [e]) | otherwise = solveEquations (Map.insert output (opfunc value1 value2) is) es where value1 = is Map.! input1 value2 = is Map.! input2 opfunc = operations Map.! operation (input1:operation:input2:_:output:[]) = e wireNumber prefix = List.filter ((prefix `List.isPrefixOf`) . fst) >>> flip zip [0..] >>> List.filter (snd . fst) >>> List.map ((2 ^ ). snd) >>> sum part1 = uncurry solveEquations >>> Map.toList >>> wireNumber "z" part2 (is, es) = List.intercalate "," . List.sort . words $ "z08 ffj dwp kfm z22 gjh jdr z31" main = getContents >>= print . (part1 &&& part2) . parseFor part 2 I tried symbolic solving to detect discrepancies but I wouldn’t achieve anything with it.
SymbolicEquation
data SymbolicEquation = Single { eqName :: String } | Combine { eqName :: String , eqOperation :: String , eqLeft :: SymbolicEquation , eqRight :: SymbolicEquation } deriving (Eq) instance Show SymbolicEquation where show (Single name) = name show (Combine name op l r) = "(" ++ name ++ "= " ++ show l ++ " " ++ op ++ " " ++ show r ++ ")" symbolicSolve is [] = is symbolicSolve is (e:es) | is Map.!? input1 == Nothing = symbolicSolve is (es ++ [e]) | is Map.!? input2 == Nothing = symbolicSolve is (es ++ [e]) | otherwise = symbolicSolve (Map.insert output (Combine output operation value1 value2) is) es where value1 = is Map.! input1 value2 = is Map.! input2 (input1:operation:input2:_:output:[]) = eMy solution was to use the
dotEngine-function to translate the operations into a digraph in graphviz-style which I simply plotted and searched through using a python script.dotEngine
dotEngine (input1:operation:input2:_:output:[]) = [ input1 ++ " -> " ++ output ++ " [ label=" ++ operation ++ "];" , input2 ++ " -> " ++ output ++ " [ label=" ++ operation ++ "];" ]I took a loook at the initial graph which was a vertical line with a few exception which I figured would be the misordered wires. I did try some hardware-simulations in the far past to build bit-adders which helped me recognize patterns like carry calculation. First I replaced all occurences of
x__ XOR y__ -> wwithx__ XOR y__ -> xor__to recognize them more easily. The same withANDof xs and ys. Using the following script I would then use some Regex to search for the rules that corresponded to carry calculations or structures I knew. The script would break exactly four times and I would then figure out what to switch by hand through looking at the updated graphViz.Please excuse the bad coding style in the script, I had written it on the ipython-REPL.
python script
r = open("input").read() for i in range(2, 45): prevI = str(i - 1).zfill(2) I = str(i).zfill(2) forward = f"xor{I} AND carry{prevI} -> (\\w+)" backward = f"carry{prevI} AND xor{I} -> (\\w+)" m1 = re.search(forward, r) m2 = re.search(backward, r) if m1 is None and m2 is None: print(forward, backward) break m = m1 or m2 r = r.replace(m.group(1), f"combinedCarry{I}") forward = f"and{I} OR combinedCarry{I} -> (\\w+)" backward = f"combinedCarry{I} OR and{I} -> (\\w+)" m1 = re.search(forward, r) m2 = re.search(backward, r) if m1 is None and m2 is None: print(forward, backward) break m = m1 or m2 r = r.replace(m.group(1), f"carry{I}") open("input", "w").write()When solving such a swapped wire problem I would then use my haskell function to plot it out again and stare at it for a few minutes until I understood wich parts belonged where.
The last one looked like this
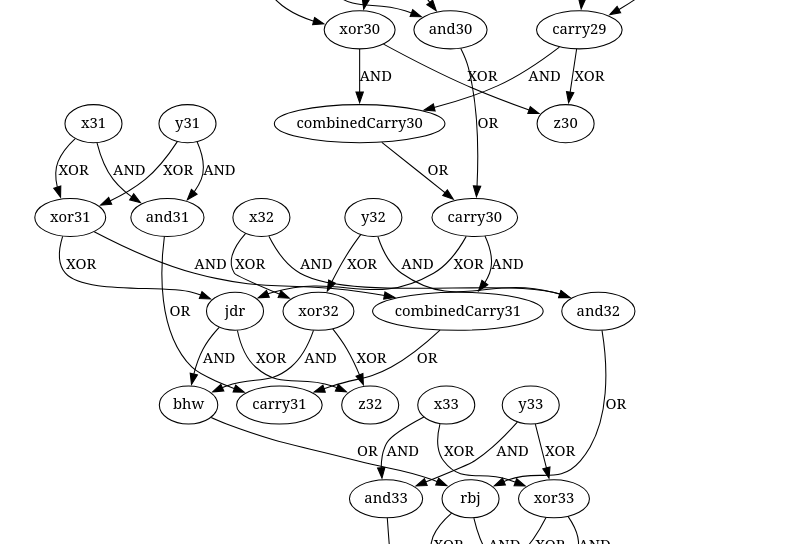
In this one I needed to switch
jdrandcarry31to make it work.





